Ch2. Vectors

[Chapter Outline]
- Scalar / Vectors
- Two / Three - dimensioned components
- Dot / Cross products

---

1. Scalars and Vectors

 

1) Scalars - aphysical quantity that is completely described by a real number.
   ex) time, mass …

 

2) Vector - both magnitude : non-negative real number & direction
   → 벡터는 크기와 방향 두 가지 값으로 존재, 벡터의 크기는 음수가 될 수 없음
   expression :  Arrow or Bold


● Graphical representation : arrows
   1) Direction of arrows → vecotors direction.
   2) Length of arrows : vector magnitude


● Vector addition
   1) Direction vector : 
   2) Distance of travel : 

   3) 2nd displacement : 
   4) The final after the two displacement : 
        (2개의 변위의 최종위치나 상태)

 

   5) Triangle rule : tail and head

 

 

 

   6) Parallelogram rule : 
       (평행사변형 법칙)

 

 

 

  ○ Commutative :  
       (교환법칙 성립)

 

  ○ Associative : 
       (결합법칙 성립)

      

 

if the sum of 2 or more vectors = 0, they form a closed polygon.
     (2개 이상 벡터의 합이 0이면 → 그 벡터들은 닫혀있는 다각형을 만들어냄)  
(사진)

Unit Vectors : 
- magnitude : 1 
- specifies a directions 

- (사진) : 크기가 1인 unit vector을 표기할 때 e위에 hat 처럼 표기해 붙일 것!

 

 

 

 

 

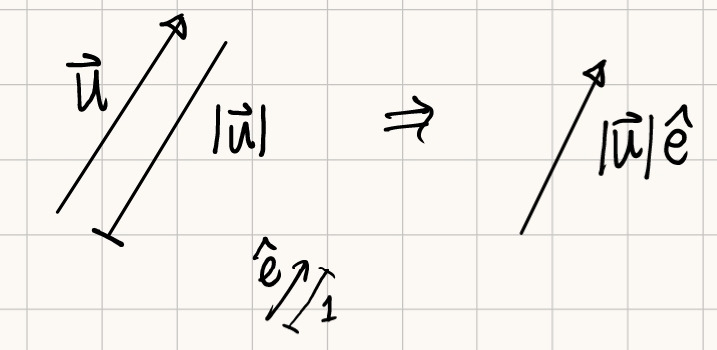
Example) 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

2. 2D components

 

● Vectors are much easier to work with when expressed in terms of mutually perpendicular vector components.
 → Vector를 2D 차원에서 두 개의 수직인 축(x,y)으로 성분으로 나누어 표현하면 다루기 쉽다.
- Carteisan coordinate system x-y coordinate(=coord’)
- U = sum of perpendicular vector components (U = Ux & Uy)

 

 

 

 

 

 

 

 

 

 

위와 같이, Vector U 를 x,y 서로 수직(Perpendicular)인 두 개의 축에 대한 두 가지의 성분의 합으로, 쪼개어 표현할 수 있다.

 

 

첫 번째는 U를 x,y 성분으로 쪼개고, 방향(벡터) 까지 표현한 것
두 번째는 벡터 U의 크기를 표현, perpendicular 성분 두 가지의 제곱의 합에 루트 씌우면 크기가 나온다.



● Manipulating vectors in terms of components : 

→ Expressing vectors in terms of their components makes it easier to perform vector addition, subtraction, or other operations.
(벡터를 성분으로 나눌 때, 다양한 연산 : 덧셈, 뺄셈, 기타 등 이 더 쉽게 가능해질 수 있다.)